ref:
https://codingopera.tistory.com/67
깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) [초등학생도 이해하는 파이썬]
안녕하세요 '코딩 오페라'블로그를 운영하고 있는 저는 'Master.M'입니다. 저는 현재 '초등학생도 이해하는 파이썬'이라는 주제로 파이썬(python)에 대해 포스팅을 하고 있습니다. 제목처럼 진짜 핵
codingopera.tistory.com
깊이 우선 탐색(DFS)
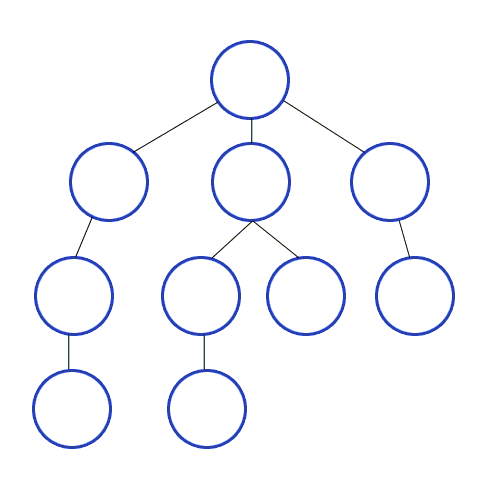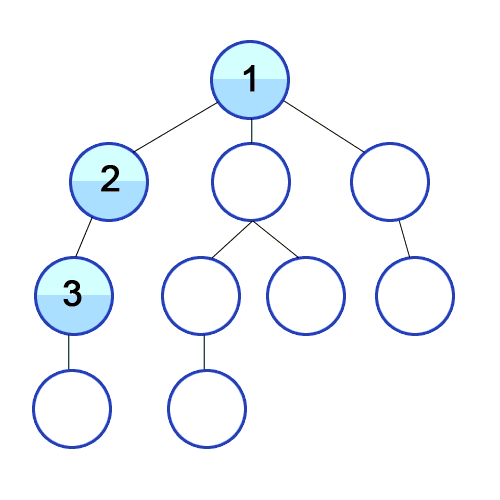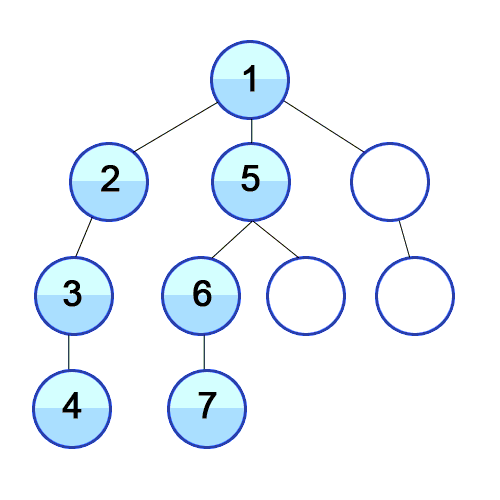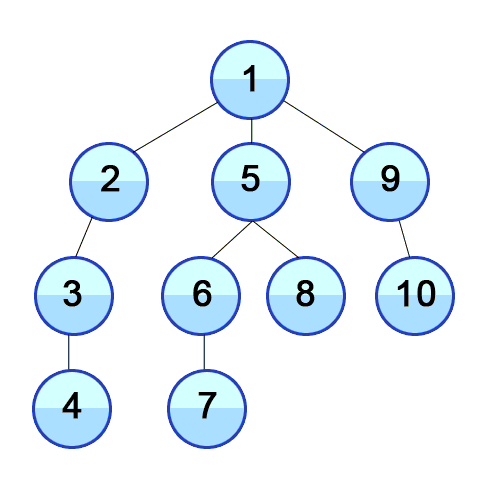
깊이 우선 탐색(DFS)
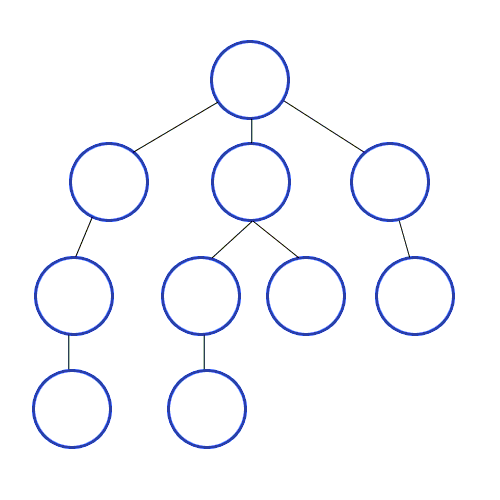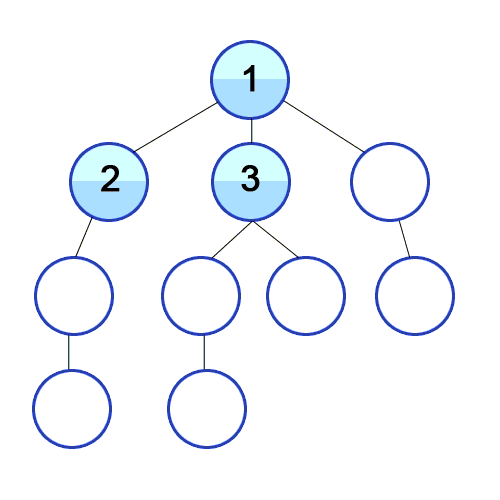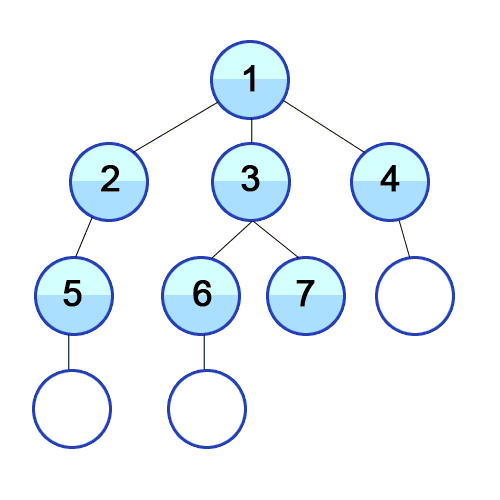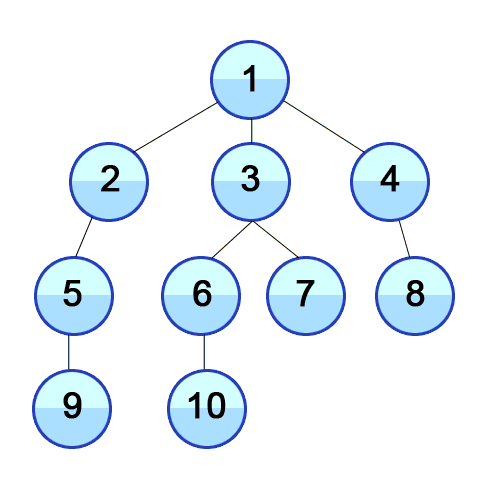
깊이 우선 탐색은 영어로 DFS(Depth Frist Search)으로 깊이를 우선으로 탐색하는 방법입니다. 위 그림과 같이 DFS는 최대한 깊이 내려간 뒤 더 이상 내려갈 곳이 없으면 옆으로 이동하는 방식을 의미합니다.
DFS는 다음과 같은 특징을 가지고 있습니다.
- 모든 노드를 방문하고자 할때 사용되는 방법
- DFS는 BFS(너비 우선 탐색)에 비해 비교적 간단함
- 검색 속도는 DFS가 BFS에 비해 느림
- 스택이나 재귀함수를 이용하여 구현
너비 우선 탐색 (BFS)
너비 우선 탐색 (BFS)
너비 우선 탐색은 영어로 BFS(Breadth Frist Search)으로 너비를 깊이보다 우선적으로 탐색하는 방법입니다. 위 그림과 같이 BFS는 최대한 옆으로 넓게 이동한 뒤 더 이상 옆으로 갈 수 없으면 아래로 이동하는 방식을 의미합니다.
BFS는 다음과 같은 특징을 가지고 있습니다.
- 최단 경로를 찾고자 할때 사용 : 위 그림과 같이 BFS는 수평으로 탐색하는 방법이기 때문에 [1-3-7], [1-4-8]과 같은 최단 경로를 중간에 찾을 수 있습니다.
- 예를 들어 A와 B 사이의 관계를 알고 싶을 때 DFS의 경우 모든 경우를 고려해야 될 수도 있지만, BFS는 가까운 관계부터 탐색을 할 수 있습니다.
- 큐를 이용하여 구현
지금까지는 DFS와 BFS의 개념에 대해 알아보았습니다. 이제부터는 이 부분의 이해를 돕고자 파이썬 예제를 보여드리겠습니다.

그래프
먼저 위와 같은 그래프가 있을 때, 이를 파이썬 딕셔너리로 표현하면 다음과 같습니다.
myGraph = {
'A': ['B', 'C', 'D'],
'B': ['A', 'E'],
'C': ['A', 'F', 'G'],
'D': ['A', 'H'],
'E': ['B', 'I'],
'F': ['C', 'J'],
'G': ['C'],
'H': ['D'],
'I': ['E'],
'J': ['F']
}
"""
DFS(Depth-First Search)
"""
def my_dfs(graph, start_node):
visited = list() # 방문한 노드를 담을 배열
stack = list() # 정점과 인접한 방문 예정인 노드를 담을 배열
stack.append(start_node) # 처음에는 시작 노드 담아주고 시작하기.
while stack: # 더 이상 방문할 노드가 없을 때까지.
node = stack.pop() # 방문할 노드를 앞에서 부터 하나싹 꺼내기.
if node not in visited: # 방문한 노드가 아니라면
visited.append(node) # visited 배열에 추가
# stack.extend(graph[node]) # 해당 노드의 자식 노드로 추가
stack.extend(reversed(graph[node]))
print("dfs - ", visited)
return visited
# 함수 실행
my_dfs(myGraph, 'A')
dfs - ['A', 'B', 'E', 'I', 'C', 'F', 'J', 'G', 'D', 'H’]- 대표적인 DFS 코드 -> 스택과 재귀함수로 구현됨.
- 처음 방문했는지 확인하기위한 변수 Visited, 연관성을 알기위한 stack을 생성
- stack에 알고싶은 문자를 대입하고시작
- while stack을 도는데 이 때 x = stack.pop해서 담겨저 있는 문자를 뺴서 비교하기 시작함
- if x not in visited:이면 visited에 추가
- stack.append(reversed(array[x])) -> pop 함수는 뒤에서 부터 불러오므로 다음과 같이 해줘야함
https://www.acmicpc.net/problem/2667
2667번: 단지번호붙이기
<그림 1>과 같이 정사각형 모양의 지도가 있다. 1은 집이 있는 곳을, 0은 집이 없는 곳을 나타낸다. 철수는 이 지도를 가지고 연결된 집의 모임인 단지를 정의하고, 단지에 번호를 붙이려 한다. 여
www.acmicpc.net
import sys
from collections import deque
input = sys.stdin.readline
N = int(input())
graph = [] # 입력받을 그래프를 담을 리스트 선언
result = [] # 결과를 담을 리스트 선언
count = 0
for _ in range(N):
graph.append(list(map(int, input().rstrip())))
# 한 점을 기준으로 (위 아래 왼쪽 오른쪽) 으로 한칸 씩 이동할 좌표 설정
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
def dfs(x, y):
global count
if x < 0 or x >= N or y < 0 or y >= N:
return
if graph[x][y] == 1:
count += 1
graph[x][y] = 0
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
dfs(nx, ny)
# 그래프의 원소가 1일때만 dfs로 집을 방문한다.
for i in range(N):
for j in range(N):
if graph[i][j] == 1:
dfs(i, j)
result.append(count)
count = 0
result.sort() # 오름차순으로 정렬
print(len(result)) # 총 단지수 출력
for k in result: # 각 단지마다 집의 수 출력
print(k)import sys
input = sys.stdin.readline
# graph = [[0, 1, 1, 0, 1, 0, 0], [0, 1, 1, 0, 1, 0, 1], [1, 1, 1, 0, 1, 0, 1], [0, 0, 0, 0,
# 1, 1, 1], [0, 1, 0, 0, 0, 0, 0], [0, 1, 1, 1, 1, 1, 0], [0, 1, 1, 1, 0, 0, 0]]
# 변수 생성, 주변 집체크용 count, 그래프, 그래프 결과값 리턴용 result
count = 0
graph, result = [], []
# 입력
N = int(input())
for _ in range(N):
yarray = list(map(int, input().strip()))
graph.append(yarray)
dx = [0,0,1,-1] # x방향
dy = [1,-1,0,0] # y 방향
# 주변 연결된 집찾기
def dfs(x, y):
global count
if x < 0 or y < 0 or x >= N or y >= N:
return
if graph[x][y] == 1:
count += 1
graph[x][y] = 0
for tt in range(len(dx)): # 0, 1, 2, 3
nx = x + dx[tt]
ny = y + dy[tt]
dfs(nx, ny)
for i in range(N):
for j in range(N):
if graph[i][j] == 1:
dfs(i, j)
result.append(count)
count = 0
result.sort()
print(len(result))
for t in result:
print(t)- 알고리즘을 작성할 때는 처음 메인 입력과 출력까지 전부 작성해둔 뒤 마지막으로 세부알고리즘을 구현해야함.
- 여기서 핵심은 dfs 문제 이해가 어느정되 되었지만 반복학습이 필요예정
- 처음 dfs 정하기 전에 방향을 dx, dy 방향을 설정함 dx[0 0 1 -1] ,dy [1 -1 0 0]
- 이후 입력받은 dfs 그래프 값을 개별 노드로 대입함.
- def dfs(x, y):
- if x < 0 or x >= N or y < 0 or y >= N 거리 벗어나면 -> 예외처리
- return
- if graph[x][y] == 1:
- count +=1 -> 방문 카운트
- graph[x][y] = 0 -> 방문했으면 0으로 처리
- for t in range(len(dx)): -> 4가지 방향 체크
- nx = x + dx[i] -> 다음 x 방향
- ny = y + dy[i] -> 다음 y 방향
- dfs(nx,ny) -> 다음방향을 받아서 주변에 1을 체크하는 재귀함수로 체크
- if x < 0 or x >= N or y < 0 or y >= N 거리 벗어나면 -> 예외처리
- def dfs(x, y):
https://www.acmicpc.net/problem/10026
10026번: 적록색약
적록색약은 빨간색과 초록색의 차이를 거의 느끼지 못한다. 따라서, 적록색약인 사람이 보는 그림은 아닌 사람이 보는 그림과는 좀 다를 수 있다. 크기가 N×N인 그리드의 각 칸에 R(빨강), G(초록)
www.acmicpc.net
# 실험중
import sys
input = sys.stdin.readline
N = int(input())
graph, cgraph= [], []
# graph = [['R', 'R', 'R', 'B', 'B'], ['G', 'G', 'B', 'B', 'B'], ['B', 'B', 'B', 'R', 'R'], ['B', 'B', 'R', 'R', 'R'], ['R', 'R', 'R', 'R', 'R']]
rgb = {}
count = 0
for _ in range(N):
array = list(map(str, input().strip()))
graph.append(array)
cgraph.append(array)
for i in range(N):
for j in range(N):
if cgraph[i][j] == "G":
cgraph[i][j] = "R"
print(graph, cgraph) # 코드는 다작성했고 내일 crgaph 변환만 확인하면 됨.
dx = [0,0,1,-1]
dy = [1,-1,0,0]
def dfs(x, y, temp):
if x < 0 or x >= N or y < 0 or y >= N:
return
if graph[x][y] == temp:
graph[x][y] = "0"
for tt in range(len(dx)):
nx = x + dx[tt]
ny = y + dy[tt]
dfs(nx, ny, temp)
def check(graph):
r, g, b = 0,0,0
for i in range(N):
for j in range(N):
rrr = "R"
bbb = "B"
ggg = "G"
if graph[i][j] == rrr:
r += 1
dfs(i, j, rrr)
rgb["R"] = r
elif graph[i][j] == bbb:
b += 1
dfs(i, j,bbb)
rgb["B"] = b
elif graph[i][j] == ggg:
g += 1
dfs(i, j, ggg)
rgb["G"] = g
# check(graph)
# print(rgb,sum(rgb.values()))- 실패
import sys
# 빠른 입력함수
input = sys.stdin.readline
# 재귀 제한 변경 -> 스택 오버플로우 발생 제한을 해결하기위해 깊이 10만정도
sys.setrecursionlimit(int(1e5))
dx = [0,0,1,-1]
dy = [1,-1,0,0]
def dfs(x, y):
for tt in range(len(dx)):
nx = x + dx[tt] # 다음 방향
ny = y + dy[tt] # 다음 방향
if nx < 0 or nx >= N or ny < 0 or ny >= N: # 예외처리
continue
if not visited[nx][ny]: # 방문하지 않았을때
if graph[x][y] == graph[nx][ny]: # 처음 bfs를 호출 할때의 x, y값으로 주변을 비교 즉 "G"가 들어왔다면 G만 비교하는 것임
visited[nx][ny] = -1
dfs(nx,ny)
N = int(input())
graph = []
for _ in range(N):
array = list(map(str, input().strip()))
graph.append(array)
# 연결 요소의 개수 세기
answer = 0
visited = [[False] * N for _ in range(N)]
for i in range(N):
for j in range(N):
if not visited[i][j]:
visited[i][j] = True
dfs(i, j)
answer += 1
print(answer, end=' ')
# 초기화
answer = 0
visited = [[False] * N for _ in range(N)]
# R -> G 변환
for i in range(N):
for j in range(N):
if graph[i][j] == "G":
graph[i][j] = "R"
for ii in range(N):
for jj in range(N):
if not visited[ii][jj]:
visited[ii][jj] = -1
dfs(ii,jj)
answer += 1
print(answer)- dfs에서 return 쓰지말고 continue 쓰자
- 재귀함수가 많이 필요할 것 같으면 "sys.setRecursion(int(1e5))" 사용 -> 10만
- 이전 나의 코드와 가장 큰 차이는, 나는 입력받은 "graph"를 건드려서 계속 사용했고, 여기는 "visited"로 방문처리를 하여 사용함
- 처음 입력을 받고 난뒤 바로 방문처리를 위한 변수를 생성함 [[False] * N for _ in range(N)]
- 지역을 알기위한 answer 변수또한 생성.
- 이후 방문을 확인하는데
- for i in range(N):
- for j in range(N):
- if not visited[i][j]: -> 방문하지 않았따면
- visited[i][j] -> 방문처리
- dfs(i, j)
- answer +=1
- if not visited[i][j]: -> 방문하지 않았따면
- for j in range(N):
- for i in range(N):
- def dfs(i,j):
- for i in range(len(dx)):
- nx = x + dx[i] -> 다음방향
- ny = y + dy[i]
- if nx < 0 or nx >= N or ny < 0 or ny >= 0: -> 예외처리
- return
- if not visited[nx][ny]:
- if graph[x][y] == graph[nx][ny]: # 즉 "G"가 들어왔다면 계속 G만 찾는거임
- visited[nx][ny] = -1 # 방문처리
- dfs(nx, ny)
- if graph[x][y] == graph[nx][ny]: # 즉 "G"가 들어왔다면 계속 G만 찾는거임
- for i in range(len(dx)):
https://www.acmicpc.net/problem/1240
1240번: 노드사이의 거리
첫째 줄에 노드의 개수 $N$과 거리를 알고 싶은 노드 쌍의 개수 $M$이 입력되고 다음 $N-1$개의 줄에 트리 상에 연결된 두 점과 거리를 입력받는다. 그 다음 줄에는 거리를 알고 싶은 $M$개의 노드 쌍
www.acmicpc.net
import sys
# 빠른 입력함수
input = sys.stdin.readline
# 재귀 제한 변경 -> 스택 오버플로우 발생 제한을 해결하기위해 깊이 10만정도
sys.setrecursionlimit(int(1e5))
def dfs(x):
# x의 인접 노드 하나씩 체크
for data in graph[x]:
# print("data:", data)
y = data[0]
cost = data[1] # x에서 y로 가는 간선 비용
if not visited[y]:
visited[y] = True
distance[y] = distance[x] + cost
dfs(y)
# n 노드의 개수, m 간선의 개수
n, m = map(int ,input().split())
# 트리 정보
graph = [[] for _ in range(n+1)]
for i in range(n-1): # 항상 트리형식이므로 간선의 개수는 n-1이다.
# 노드 a와 노드 b가 연결 (간선 비용은 c)
a, b, c = map(int, input().split())
graph[a].append((b, c))
graph[b].append((a, c))
print(graph)
# 각 쿼리마다 매번 dfs를 수행
for i in range(m):
# x에서 y로 가기위한 최단 거리 계산
x, y = map(int, input().split())
# 방문 여부 및 최단 거리 테이블 초기화
visited = [False] * (n+1)
distance = [-1] * (n+1)
visited[x] = True # 시작점 방문 처리
distance[x] = 0 # 자신까지의 거리는 0
dfs(x) # x부터의 치단 거리 계산
print(distance[y])'CoTe > fastcampus' 카테고리의 다른 글
| 21. BFS를 활용한 그래프 탐색 알고리즘 - 핵심 유형 문제 풀이(3) (0) | 2024.04.03 |
|---|---|
| 08. 고급 탐색 알고리즘 - 핵심 유형 문제풀이 - 힙, 자료구조 (0) | 2024.03.19 |
| 07. 고급 탐색 알고리즘 - 기초 문제풀이 - 트리 (0) | 2024.03.19 |
| 06. 기본 탐색 알고리즘 - 핵심 유형 문제풀이 - 이진 탐색 (0) | 2024.03.16 |
| 05. 기본 탐색 알고리즘 - 기초 문제풀이 - 탐색 (0) | 2024.03.15 |










