DepGraph: Towards Any Structural Pruning
ref:DepGraph: Towards Any Structural Pruning
오늘 리뷰할 자료는 모델 경량화 기법중 하나인 Structural Pruning이다. 아직 정식으로 출판은 되지 않았고 2023 cvpr에서 발표될 예정이라고 한다. 따라서 발표전 arxiv에 있는 논문을 바탕으로 리뷰를 진행한다.
저자인 현재 Gongfan Fang친구는 현재 박사 1년차라고 하네요[https://github.com/VainF]
Abstract
Structural pruning 신경망에서 구조적으로 그룹화된 매개 변수를 제거하여 모델 가속화를 가능하게 한다. 그러나 매개 변수 그룹화 패턴은 다양한 모델에 걸쳐 매우 다양하며, 수동으로 설계된 그룹화 체계에 의존하는 아키텍처를 새로운 아키텍처에 대해 일반화할 수 없는 특정 가지치기로 만든다.
본 연구에서는 CNN, RNN, GNN 및 Transformer와 같은 임의 아키텍처의 일반적인 구조 가지치기를 다루기 위해 매우 어렵지만 거의 탐구되지 않은 모든 구조 가지치기 작업을 연구한다. 이 목표를 향한 가장 큰 장애물은 structural coupling에 있는데, 이는 서로 다른 계층을 동시에 제거하도록 강요할 뿐만 아니라 제거된 모든 매개 변수가 일관되게 중요하지 않을 것으로 예상하여 제거 후 구조적 문제와 상당한 성능 저하를 방지한다.
이 문제를 해결하기 위해 계층 간의 종속성을 명시적으로 모델링하고 가지치기를 위해 결합된 매개 변수를 포괄적으로 그룹화하는 일반적이고 완전 자동으로 사용할 수 있는 방법인 Dependency Graph(DepGraph)를 제안한다. 본 연구에서는 ResNe(X)t, DenseNet, MobileNet 및 Vision transformer(이미지용), GAT(그래프용), GAT(3D 포인트 클라우드용), DGCNN(언어용)을 포함한 여러 아키텍처 및 작업에 대한 방법을 광범위하게 평가하고 language를 위한 LSTM과 함께 이를 입증한다.
Introduction

최근 에지 컴퓨팅 애플리케이션의 출현은 심층 신경 압축의 필요성을 요구한다. 많은 네트워크 압축 패러다임 중에서 pruning 는 매우 효과적이고 실용적인 것으로 입증되었다.
1. Network pruning의 목표는 주어진 네트워크에서 중복 매개 변수를 제거하여 그 크기를 가볍게 하고 잠재적으로 추론 속도를 높이는 것. 2. structurual pruning은 grouped parameters를 물리적으로 제거하여 신경망의 구조를 변경한다 [Mainstream pruning 접근법] 3. unstructural pruning는 네트워크 구조를 수정하지 않고 부분 가중치에 대해 제로화(zeroing)을 수행한다는 것. [Mainstream pruning 접근법] Unstructural pruning에 비해 Structurual pruning는 메모리 소비와 계산 비용을 줄이기 위해 특정 AI 가속기나 소프트웨어에 의존하지 않으므로 실제로 더 넓은 응용 분야를 찾는다.
그럼에도 불구하고 Structurual pruning의 특성 자체는 특히 내부 구조가 복잡하고 결합된 현대의 심층 신경망에서 어려운 작업이 된다. 이론적 근거는 심층 신경망이 컨볼루션, 정규화 또는 활성화와 같은 많은 수의 기본 모듈을 기반으로 구축되지만 이러한 모듈은 매개 변수화 여부에 관계없이 복잡한 연결을 통해 본질적으로 결합된다는 것이다. 결과적으로 그림 1(a)에 표시된 CNN에서 하나의 채널만 제거하려고 할 때에도 모든 계층에 대한 상호 종속성을 동시에 처리해야 한다. 그렇지 않으면 결국 네트워크가 끊어지게 되는데, 정확히 말하면 residual connection은 동일한 수의 채널을 공유하기 위해 두 개의 컨벌루션 레이어의 출력을 필요로 하므로 강제로 함께 잘라내야 한다. 그림 1(b-d)에 표시된 것처럼 트랜스포머, RNN 및 GNN과 같은 다른 아키텍처의 구조 가지치기도 마찬가지이다.
불행하게도, 종속성(dependency)은 residual structures에서만 나타나는 것이 아니며, 현대 모델에서는 무한히 복잡할 수 있다. 기존의 structural 접근 방식은 네트워크의 dependencies을 처리하기 위해 사례별 분석에 크게 의존했다. 달성된 유망한 결과에도 불구하고 이러한 네트워크별 가지치기 접근 방식은 많은 노력이 필요하다. 더욱이 이러한 방법은 직접 일반화할 수 없다. 즉, 수동으로 설계된 그룹화 체계(manually-designed grouping)는 다른 네트워크 제품군 또는 동일한 제품군의 네트워크 아키텍처로 이전할 수 없으므로 산업 응용 프로그램이 크게 제한된다.
본 논문에서, 임의의 네트워크 아키텍처에 대한 structural pruning이 자동 방식으로 실행되는 모든 structural pruning에 대한 일반적인 체계를 위해 노력한다. 접근 방식의 핵심은 신경망에서 쌍을 이룬 계층 간의 상호 Dependency을 명시적으로 모델링하는 Dependency Graph(DepGraph)를 추정하는 것이다.
또한 structural pruning에서 그룹화된 레이어가 동시에 pruning되므로 동일한 그룹에서 제거된 모든 매개변수가 일관되게 중요하지 않을 것으로 예상된다. 이는 단일 계층에 대해 설계된 기존 중요도 기준에 특정한 어려움을 가져온다. 정확히 말하면 단일 레이어의 매개변수 중요도는 다른 매개변수화된 레이어와의 얽힘으로 인해 더 이상 올바른 중요도를 나타내지 않는다. 이 문제를 해결하기 위해 DepGraph에서 제공하는 종속성 모델링의 포괄적인 기능을 최대한 활용하여 "grouplevel" 중요도 기준을 설계한다. 이 기준은 그룹 내에서 일관된 희소성(sparsity)을 학습하므로 성능이 크게 저하되지 않고 제로화(zeroized)된 그룹을 안전하게 제거할 수 있다.
DepGraph의 효과를 검증하기 위해 제안된 방법을 CNN, Transformers, RNN, GNN를 포함한 여러 인기 아키텍처에 적용하여 최첨단 방법에 비해 경쟁력 있는 성능을 달성한다. CNN 가지치기의 경우, 제안한 방법은 CIFAR에서 93.64%의 정확도를 가진 2.57배 가속 ResNet-56 모델을 얻는데, 이는 93.53%의 정확도를 가진 가지치기되지 않은 모델보다 더 우수. 또한 ImageNet-1k에서 우리의 알고리듬은 ResNet-50에서 2배 이상의 속도 향상을 달성하며 성능은 0.32%만 손실됨. 더 중요한 것은 우리의 방법이 ResNe(X)t, DenseNet, VGG, MobileNet, GoogleNet 및 Vision Transformer를 포함하여 다양한 인기 있는 네트워크로 쉽게 이전될 수 있으며 만족스러운 결과를 보여줄 수 있다는 것이다. 또한 텍스트 분류를 위한 LSTM, 3D 포인트 클라우드를 위한 DGCNN, 그래프 데이터를 위한 GAT를 포함하여 비이미지 신경망에 대한 추가 실험을 수행하며, 이 방법은 성능 저하 없이 8배에서 16배까지 가속화된다.
Related Work
Structural and Nonstructural Pruning.
Pruning은 다양한 문헌에서 입증된 바와 같이 네트워크 가속 분야에서 엄청난 발전을 이루었다. Mainstream pruning 방법은 structural pruning과 unstructural pruning의 두 가지 유형으로 크게 분류할 수 있다. Structural pruning은 매개변수 그룹을 물리적으로 제거하여 신경망의 크기를 줄이는 것을 목표로 한다. 대조적으로 unstructural pruning는 네트워크 구조를 변경하지 않고 특정 가중치를 0으로 만드는 것을 포함한다. 실제로 unstructural pruning은 특히 구현이 간단하고 본질적으로 다양한 네트워크에 적응할 수 있다. 그러나 모델 가속을 위해 전문 AI 가속기 또는 소프트웨어가 필요한 경우가 많다. 반대로 Structural pruning는 네트워크에서 매개변수를 물리적으로 제거하여 inference 오버헤드를 개선하여 더 넓은 응용 분야를 찾는다. 다양한 문헌에서 pruning 알고리즘의 설계 공간은 pruning schemes(계획) 방식, 매개변수 선택, 계층 희소성(layer sparsity) 및 training techniques을 포함한 다양한 측면을 포함한다 . 최근 몇 년 동안 크기 기반 기준(magnitude-based criteria), 기울기 기반 기준(gradient-based criteria) 및 학습된 희소성(learned sparsity)과 같은 수많은 강력한 기준이 도입되었다.
Pruning Grouped Parameters.
복잡한 네트워크 구조에서 매개변수 그룹 간에 종속성(dependencies)이 발생할 수 있으므로 동시 제거가 필요하다. 결합 매개변수(coupled parameter)의 pruning은 structural pruning 초기부터 연구의 초점이었다. 예를 들어, 두 개의 연속적인 컨볼루션 레이어를 정리할 때 첫 번째 레이어에서 필터를 제거하면 후속 레이어에서 관련 커널을 정리해야 한다. 매개변수 dependencies를 수동으로 분석하는 것이 가능하지만 이 프로세스는 많은 이전 연구에서 설명한 것처럼 복잡한 네트워크에 적용할 때 매우 노가다이다. 게다가, 그러한 수작업 체계는 본질적으로 pruning의 적용을 심각하게 제한하는 새로운 아키텍처로 이전할 수 없다. 최근에 레이어 간의 복잡한 관계를 해독하기 위한 일부 파일럿 작업이 제안되었다. 불행하게도 기존 기술은 여전히 경험적 규칙이나 미리 정의된 아키텍처 패턴에 의존하므로 모든 구조 가지치기 응용 프로그램에 다용성이 부족하다. 이 연구에서 우리는 이 문제를 해결하기 위한 일반적인 접근 방식을 제시하고 매개 변수 dependencies를 해결하면 광범위한 네트워크에서 structural pruning를 효과적으로 일반화하여 여러 작업에서 만족스러운 성능을 얻을 수 있음을 보여준다.
Method
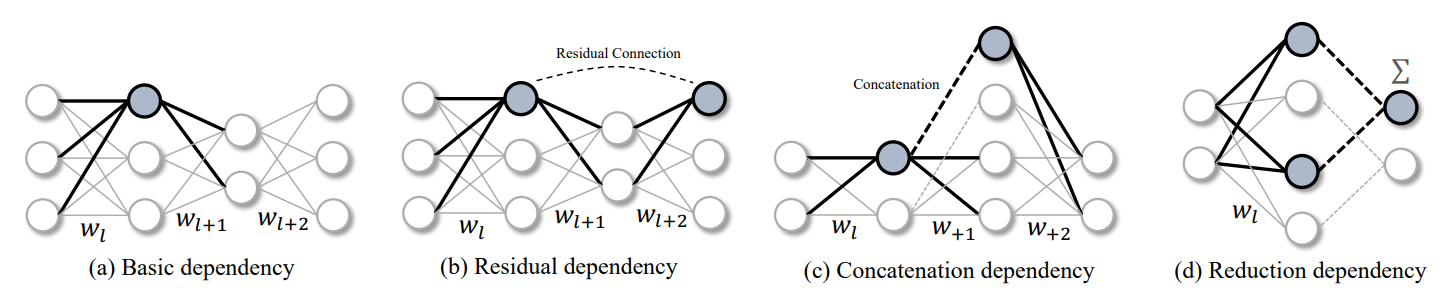
3.1. Dependency in Neural Networks
현재 파트에서는 매개변수 종속성의 제한 하에서 모든 신경망의 구조적 가지치기에 중점을 둔다. 그림 2(a)(Basic dependency)와 같이 각각 2D 가중치 행렬 wl , wl+1 및 wl+2로 매개변수화된 3개의 연속 레이어로 구성된 선형 신경망을 보면 일반성(generality)을 잃지 않고 완전 연결(FC) 계층에서 방법을 개발함
- 그림 2(a)(Basic dependency)와 같이 각각 2D 가중치 행렬 wl , wl+1 및 wl+2로 매개변수화된 3개의 연속 레이어로 구성된 선형 신경망부터 시작
- 이 간단한 신경망은 뉴런 제거를 통한 구조적 가지치기로 슬림하게 만들 수 있다. 이 경우 wl <-> wl+1로 표시되는 매개변수 사이에 일부 종속성이 나타나 wl과 wl+1이 동시에 제거되도록 하는 것을 쉽게 찾을 수 있다. 구체적으로, wl과 wl+1을 연결하는 k번째 뉴런을 잘라내기 위해 wl [k, :]와 wl+1[:, k]가 모두 제거된다.
- 이전 논문들을 보면 연구원들은 layer dependencies을 처리하고 수동으로 설계된 모델별 체계로 심층 신경망에서 구조적 가지치기를 가능하게 한다.
- 그럼에도 불구하고 그림 2(b-d)에 표시된 것처럼 많은 종류의 종속성이 있다.
- simple dependencies을 중첩 하거나 구성하여 더 복잡한 패턴을 형성할 수 있는 것은 말할 것도 없고 모든 종속성을 사례별로 수동으로 분석하는 것은 다루기 어렵다.
- structural pruning의 dependency문제를 해결하기 위해 이 작업에서 dependency 모델링을 위한 일반 및 완전 자동 메커니즘을 제공하는 Dependency Graph를 도입
3.2. Dependency Graph
Grouping
structural pruning를 활성화하려면 먼저 상호 종속성(inter-dependency)에 따라 레이어를 그룹화해야 한다. 공식적으로, 목표는 그룹화 행렬 G∈ RL×L을 찾는 것이다. 여기서 L은 제한될 네트워크의 레이어 수를 나타내고 Gij = 1은 i번째 레이어와 j번째 레이어 사이의 종속성의 존재를 나타낸다.
편의를 위해 self-dependency을 가능하게 하기 위해 Diag(G) = 1 1×L로 둔다. 그룹화 행렬( G∈ RL×L)을 사용하면 g(i)로 표시되는 i번째 계층에 대한 상호 종속성이 있는 모든 결합 계층을 쉽게 찾을 수 있다.

그럼에도 불구하고 신경망에서 그룹화 패턴을 추정하는 것은 쉬운 일이 아니다. 현대의 심층 네트워크는 복잡한 연결을 가진 수천 개의 레이어로 구성되어 크고 복잡한 그룹화 행렬 G를 생성할 수 있기 때문이다.
이 행렬에서 Gij는 다음과 같다.
- i번째 및 j번째 레이어에 의해 결정될 뿐만 아니라 그들 사이의 중간 레이어에 의해 영향을 받는다. 따라서 이러한 non-local고 암묵적인 관계(implicit relations)는 대부분의 경우 간단한 규칙으로 처리할 수 없다.
- 이 문제를 극복하기 위해 그룹화 행렬(grouping matrix) G를 직접 추정하지 않고 dependency modeling을 위한 동등하지만 추정하기 쉬운(easy-to estimate) 방법, 즉 G를 효율적으로 파생할 수 있는 Dependency Graph를 제안.
Dependency Graph
- w1 ⇔ w2, w2 ⇔ w3 및 w1 ⇔ w3 종속성을 갖는 그룹 g = {w1, w2, w3}을 고려하여 시작한다.
- 이 종속성 모델링을 면밀히 살펴보면 일부 중복성이 있음을 관찰할 수 있다.
- 예를 들어 w1 ⇔ w3 종속성은 w1 ⇔ w2 및 w2 ⇔ w3에서 재귀 프로세스(recursive process)를 통해 파생될 수 있다. 처음에는 w1을 시작점으로 삼고 w1 ⇔ w2와 같은 다른 레이어에 대한 dependency을 검사. 그런 다음 w2는 dependency 을 recursively으로 확장하기 위한 새로운 시작점을 제공하며, 이는 차례로 w2 ⇔ w3을 "triggers"한다. 이 recursive process은 궁극적으로 전이 관계인 w1 ⇔ w2 ⇔ w3로 끝난다. 이 경우 그룹 g의 관계를 설명하기 위해 두 개의 종속성만 필요하다.
- 마찬가지로 섹션 3.2(dependency grapth)에서 논의된 그룹화 매트릭스도 종속성 모델링을 위해 중복되므로 동일한 정보를 유지하면서 더 적은 수의 에지로 더 압축된 형태로 압축할 수 있다. dependency grapth는 인접 레이어 간의 local inter-dependenc을 측정하는 새로운 그래프 D가 grouping matrix G에 효과적인 감소가 될 수 있음을 보여준다. Dependency Graph는 직접 연결된 인접 레이어 간의 dependencies만 기록한다는 점에서 G와 다르다.
- Graph D는 G와 동일한 꼭지점(vertices)을 포함하지만 가능한 한 적은 수의 모서리를 포함하는 G의 전이적 감소(transitive reduction)로 볼 수 있다. 공식적으로 D는 모든 Gij = 1에 대해 정점 i와 j 사이의 경로가 D에 존재하도록 구성된다. 따라서 Gij는 D에서 꼭지점 i와 j 사이의 경로 존재 여부를 조사하여 도출할 수 있다.
Network Decomposition.
그러나 fully-connected layers와 같은 일부 기본 레이어는 섹션 3.1에서 설명한 바와 같이 w[k, :] 및 w[:, k]와 같은 두 가지 다른 pruning schemes(체계)를 가질 수 있기 때문에 레이어 수준에서 dependency graph를 구축하는 것은 실제로 문제가 될 수 있다. 게다가, 네트워크에는 스킵 연결(skip connections)과 같은 non-parameterized 작업도 포함되어 있으며, 이는 계층 간의 dependency에도 영향을 미친다.
이러한 문제를 해결하기 위해 네트워크 F(x; w)를 F = {f1, f2, ..., fL}로 표시된 더 미세하고 기본적인 구성 요소로 분해하는 새로운 표기법을 제안한다. 여기서 각 구성 요소 f는 컨볼루션과 같은 parameterized layer된 레이어 또는 residual adding와 같은 non-parameterized을 참조한다.
- layer level에서 관계를 모델링하는 대신 계층의 입력과 출력 사이의 dependencies 에 집중하는데, component fi의 입력과 출력을 각각 f-i와 f+i로 나타낸다. 모든 네트워크에 대해, 최종 분해는 F = {f - 1, f + 1, ..., f - L, f + L }로 공식화될 수 있다. 이 표기법은 dependency 모델링을 용이하게 하고 동일한 layer에 대해 다른 pruning schemes (계)를 허용한다.
Dependency Modeling.

이 표기법을 활용하여 신경망을 Equation 2로 스케치한다. 여기서 두 가지 주요 유형의 dependency, 즉 계층 간 종속성(inter-layer dependency)과 계층 내 종속성(intra-layer dependency,)을 식별할 수 있다:

↔ 기호는 인접한 두 레이어 간의 연결을 나타낸다. 이 두 가지 dependency을 검사하면 dependency modeling에 대한 간단하지만 일반적인 규칙이 생성된다:
- 계층 간 종속성(inter-layer dependency): f - i ⇔ f + j의 종속성은 f - i ↔ f + j인 연결된 계층에서 지속적으로 발생한다.
- 계층 내 종속성(intra-layer dependency): f - i와 f + i가 동일한 가지치기 체계를 공유하는 경우 종속성 f - i ⇔ f + i가 존재하며, 이는 sch(f - i ) = sch(f + i)로 표시된다.
첫째, 네트워크의 위상 구조(topological structure)가 알려진 경우 inter-layer dependency을 쉽게 추정할 수 있다. f - i ↔ f + j를 가진 연결된 레이어의 경우, f - i 및 f + j가 네트워크의 동일한 중간 기능에 해당하므로 종속성이 일관되게 존재. 다음 단계에서는 계층 내 종속성을 설명. 계층 내 종속성(intra-layer dependency)은 단일 계층의 입력과 출력을 동시에 제거해야 한다. 입력과 출력이 sch(f - i) = sch(f + i)로 표시된 동일한 가지치기 체계를 공유하는 배치 정규화와 같은 많은 네트워크 계층이 이 조건을 충족하므로 그림 3에 표시된 것처럼 동시에 가지치기된다. 대조적으로, 컨볼루션과 같은 레이어는 입력과 출력에 대해 뚜렷한 가지치기 체계를 가지고 있다. 즉, w[:, k, :, :] 6= w[k, :, :, :] 그림 3과 같이 sch(f - i) 6= sch(f + i)가 된다. 이러한 경우, 컨볼루션 레이어의 입력과 출력 사이에는 의존성이 없다. 위에서 언급한 규칙을 고려할 때, 다음과 같이 공식적으로 dependency modeling 식을 세울 수 있다:

여기서 ∨ 및 ∧는 논리적 "OR" 및 "AND" 작동을 나타내며, 1은 "True"가 유지 조건임을 반환하는 표시기 함수다. 첫 번째 용어는 네트워크 연결로 인한 계층 간 종속성(Inter-layer Dependency)을 검토하고, 두 번째 용어는 계층 입력과 출력 간 공유 가지치기 체계에 의해 도입된 계층 내 종속성(intra-layer dependency)을 검토. DepGraph는 D(f - i, f + j ) = D(f + j, f - i)를 갖는 대칭 행렬이다. 따라서 모든 입출력 쌍을 검사하여 dependency graph를 추정할 수 있다. 그림 3에서, 우리는 residual connections이 있는 CNN 블록의 DepGraph를 시각화한다. 알고리즘 1과 2는 dependency modeling 및 grouping를 위한 알고리즘을 요약한다.

Group-level Pruning
이전 섹션에서는 자연스럽게 group-level pruning 문제로 이어지는 neural networks 내 dependencies을 분석하기 위한 일반적인 방법론을 개발했다. 그룹화된 매개변수의 중요성을 평가하는 것은 pruning에 여러 결합된 계층이 관련되기 때문에 중요한 문제가 된다.
이 섹션에서는 간단한 규범 기반 기준(norm-based criterion)[29]을 활용하여 group-level pruning를 위한 실용적인 방법을 설정한다. parameter group g = {w1, w2, ..., w|g|}가 주어지면 L2-표준 중요도(norm importance) I(w) = \\w\\2와 같은 기존 기준은 각 w ∈ g에 대해 독립적인 점수를 생성할 수 있다. group importance를 추정하는 자연스러운 방법은 집계 점수
I(g) = 시그마 w∈g I(w)를 계산하는 것이다.
불행하게도, 서로 다른 레이어에서 독립적(nonadditive)으로 추정된 중요도 점수는 비가산적이기 때문에 분포와 크기의 차이로 인해 의미가 없다.
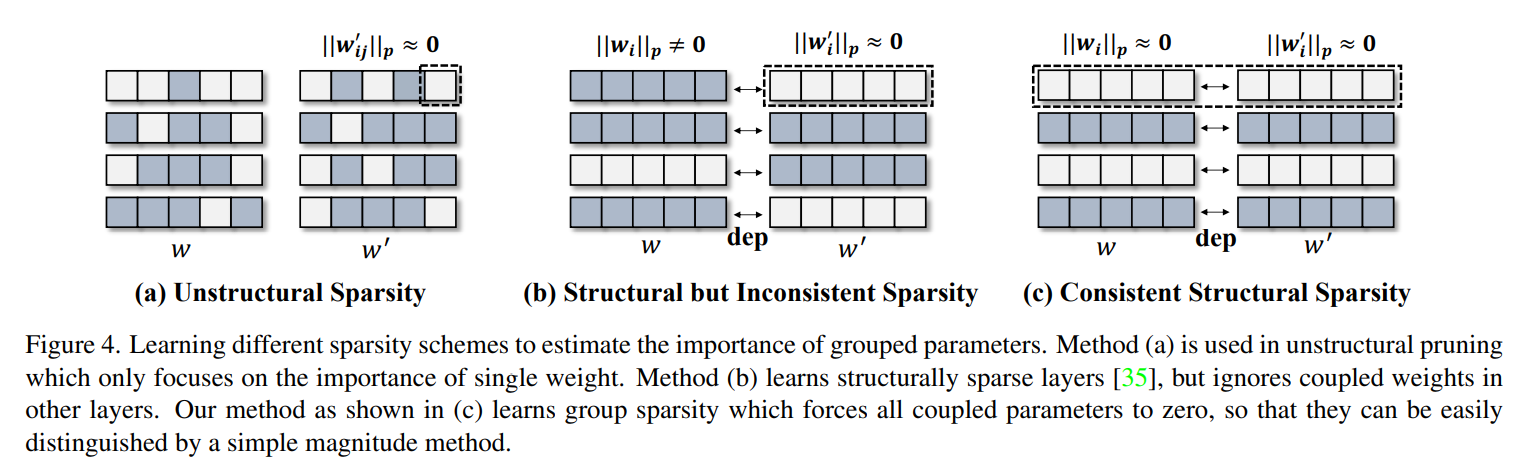
이 간단한 집계가 중요도 추정(importance estimation)을 위해 작동하도록 하려면 그림 4(c)와 같이 그룹 수준에서 매개변수를 희소화하는 희소 훈련 방법(sparse training method)을 제안한다.
이렇게 하면 zeroized groups이 네트워크에서 안전하게 제거될 수 있다. 구체적으로, w[k]로 인덱싱된 K이다 가지치기 가능한 차원이 있는 각 매개변수 w에 대해 다음과 같이 정의된 sparse training을 위한 간단한 정규화(regularization) 용어를 도입한다.

여기서 Ig,k = Pw∈gkw[k]k22는 k번째 가지치기 가능한 치수의 중요성을 나타내며, γk는 이러한 파라미터에 적용되는 수축 강도(shrinkage strength)를 나타낸다. 제어 가능한 지수 전략(controllable exponential strategy)을 사용하여 다음과 같이 µk를 결정:


여기서 정규화된 점수는 수축 강도(control the shrinkage strength) αk를 제어하는 데 사용되며, [20, 2 α]의 범위 내에서 변화한다.
이 작업에서, 우리는 모든 실험에 일정한 초 매개 변수 α = 4를 사용한다. sparse training 후, 우리는 중요하지 않은 매개 변수를 식별하고 제거하기 위해 간단한 relative score ˆIg,k = N · Ig,k/ P{TopN(Ig)}를 추가로 사용한다. 실험 섹션에서, 이러한 간단한 가지치기 방법이 일관된 sparse training과 결합될 때 현대적인 접근 방식과 유사한 성능을 달성할 수 있음을 보여준다.
Experiment

- 다양한 그룹화 전략 및 희소성 구성에 대한 CIFAR-100에 대한 절제 연구.
- 제안된 전략인 전체 그룹화는 희소 교육 동안 모든 매개 변수화된 계층을 고려하는 반면, 다른 전략은 부분 계층만 활용한다.
- 균일한 레이어 희소성 또는 학습된 레이어 희소성을 가진 제거된 모델의 정확도(%)가 보고됩니다.
- ◦:경우에 따라 제안한 방법은 일부 차원을 1로 오버 프루닝하여 최종 정확도를 심각하게 손상시킨다.



Conclusion
이 연구에서, 우리는 다양한 신경망에서 구조적 가지치기를 가능하게 하기 위해 의존성 그래프를 도한다. 본 연구는 CNN, RNN, GNN 및 트랜스포머를 포함한 아키텍처에 적용할 수 있는 일반 알고리듬을 개발하는 첫 번째 시도이다.
- 현재 논문에서 언급된 네트워크를 제외하고 추가로 YOLOv7, YOLOv8까지 현재 제공하고 있다. 아직까지는 아카이브에만 논문이 올라와 있지만 CVPR 발표 후 조금 더 인기가 있어질 것 같다.
- 구조적 가지치기를 YOLOv8 네트워크에 어떻게 제공되는지 확인을 하고 추가로 내가 필요한 부분까지 Pruning을 진행할 수 있는지 실험이 필요할 것 같다.